Locked candidates
The locked candidates is a basic sudoku solving technique that you need to master.
Principle
An intersection is a part of the grid made up of cells common to two groups of cells. The intersections that interest us here are those between rows (or columns) on the one hand, and regions on the other. In a standard sudoku grid, there are 27 intersections between rows and regions, and another 27 between columns and regions, each of these intersections being composed of three cells.
Intersection between row A and region 1, here in blue.
Two types of use of these intersections to eliminate candidates can be distinguished.
Type 1
In a region, if all the candidates of a given number are grouped in the same intersection with a row or a column, then this number can be removed as candidate from all the cells of this row or this column not doing not part of the intersection.
This first type is also called pointing pairs when the intersection contains two occurrences of the number, or pointing triples if it contains three.

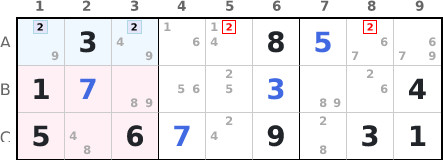
In region 1, the candidates for the number 2 are grouped in the intersection with row A.
We can therefore remove the number 2 as candidate from the cells of row A that are not part
of the intersection, here those located in regions 2 and 3.
Type 2
On a row (or column), if all the candidates of a given number are grouped in the same intersection with a region, then this number can be removed as candidate from all the cells of this region not belonging of the intersection.
This second type is also called box-line reduction or claiming.
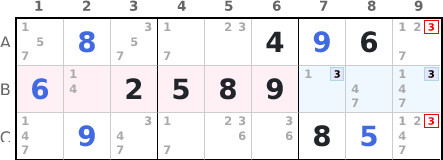
On row B, the candidates for the number 3 are grouped in the intersection with the region 3.
We can therefore remove the number 3 as candidate from the cells of the region 3 not forming
part of the intersection, here those located on rows A and C.
Examples
Example 1 : locked candidates type 1 / pointing pairs
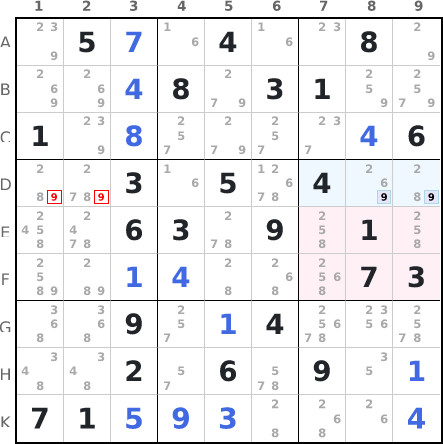
In region 6, candidates for the number 9 are clustered in the intersection with row D (D7/D8/D9). We can therefore remove the number 9 as candidate from the cells of row D not forming part of the intersection, here in D1 and D2.
Example 2 : locked candidates type 1 / pointing pairs
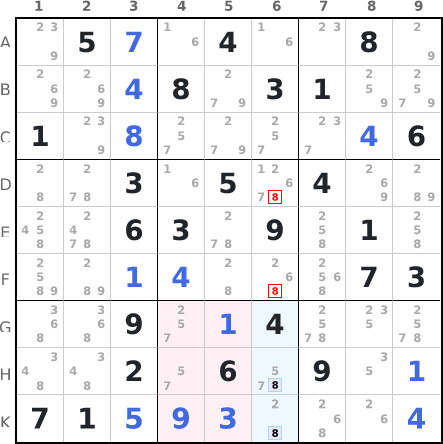
In region 8, candidates for number 8 are clustered in the intersection with column 6 (G6/H6/K6). We can therefore remove the number 8 as candidate from the cells of column 6 not forming part of the intersection, here in D6 and F6.
Example 3 : locked candidates type 2 / box-line reduction / claiming
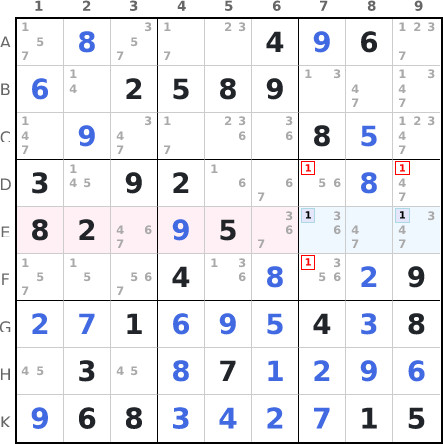
On row E, candidates for number 1 are clustered in the intersection with region 6 (E7/E8/E9). We can therefore remove the number 1 as candidate from the cells of region 6 not forming part of the intersection, here in D7, D9 and F7.
Example 4 : locked candidates type 2 / box-line reduction / claiming
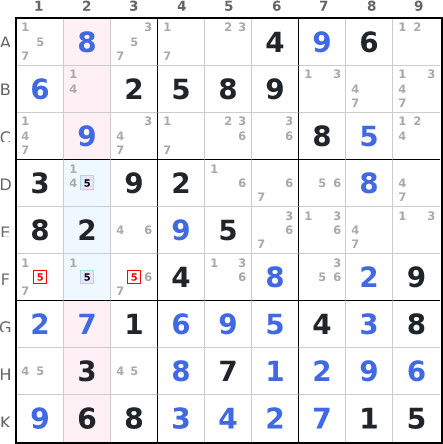
On column 2, candidates for number 5 are clustered in the intersection with region 4 (D2/E2/F2). We can therefore remove the number 5 as candidate from the cells of region 4 not forming part of the intersection, here in F1 and F3.
Exercises
These sudoku grids need to use the locked candidates technique in order to be solved :
- Sudoku n°17957 (Easy)
- Sudoku n°37347 (Medium)
- Sudoku n°576246 (Medium)
- Sudoku n°369449 (Medium)
- Sudoku n°145829 (Medium)
You can also challenge yourself with our daily sudokus, the easy and medium levels regularly contain locked candidates of both types.